Binomialverteilung mit dem Casio fx-991DE X
Inhaltsverzeichnis
\(\\\)
Binomial-Dichte
Für die Berechnung der Wahrscheinlichkeit der Binomialverteilung mit
\( \quad \begin{array}{ r c c } n & = & 10 \\ p & = & 0{,}6 \\ k & = & 4 \\ \end{array} \)
\(\\\)

bietet der Casio fx-991DE X eine einfache Funktion an.
Dazu gehen wir auf \(\boxed{MENU}\) und mit Pfeil rechts auf

\(\\\)
Wir bestätigen mit \(\boxed{=}\) .

\(\\\)
Nun wird die Binomial-Dichte mit \(\boxed{4}\) ausgewählt

\(\\\)
und weiter Variable mit \(\boxed{2}\) .

\(\\\)
Es erfolgt die Eingabe der Werte, wobei jede Eingabe mit \(\boxed{=}\) bestätigt wird. Zum Schluß wird noch einmal \(\boxed{=}\) eingegeben.

\(\\[1em]\)
Liste
Über die Liste lassen sich mehrere Werte auf einmal berechnen.
\( \quad \begin{array}{ r c l } n & = & 20 \\ p & = & 0{,}6 \\ k & = & 14 , \, 15 , \, 16 \\ \end{array} \)
\(\\\)

\(\\\)
Wir starten in dem Menu der Verteilungsfunktionen

\(\\\)
und geben \(\boxed{4}\) ein.

\(\\\)
Wir wählen Liste mit \(\boxed{1}\)

\(\\\)
und geben die \(k\)-Werte ein. Dabei bestätigen wir jede Eingabe mit \(\boxed{=}\) .

\(\\\)
Nach der letzten Eingabe betägigen wir abermals die \(\boxed{=}\) -Taste.

\(\\\)
Wir geben die Werte für \(n\) und \(p\) ein. Dabei bestätigen wir jede Eingabe mit \(\boxed{=}\) . Nach der letzten Eingabe betägigen wir abermals die
\(\boxed{=}\) -Taste.

\(\\\)
Für die Wahrscheinlichkeit von \(14\) bis \(16\) Treffer gilt
\( \quad \begin{array}{ r c l } P(14 \leq x \leq 16) & = & P(x = 14) + P(x = 15) + P(x = 16) \\[4pt] & = & 0{,}1244 + 0{,}0746 + 0{,}0349 \\[4pt] & = & 0{,}2339 \\[4pt] & = & 23{,}39\% \\ \end{array} \)
\(\\[1em]\)
Kumulierte Binomial-Verteilung
Das eben berechnete Beispiel kann auch mit der kumulierten Wahrscheinlichkeit berechnet werden. Die Wahrscheinlichkeit mit
\( \quad \begin{array}{ r c l } n & = & 20 \\ p & = & 0{,}6 \\ k & \leq & 16 \\ \end{array} \)
\(\\\)
und
\( \quad P( x \leq 16) \)

\(\\\)
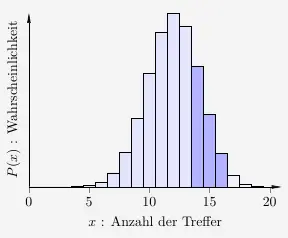
berechnet alle Werte bis \(16\). Um die Werte von \(14\) bis \(16\) zu berechnen,
\(\\\)
wird der Bereich davor abgezogen. Damit ergibt sich
\( \quad P( 14 \leq x \leq 16) \, = \, P( x \leq 16) - P( x \leq 13) \)
\(\\\)
Mit dem Taschenrechner berechnen wir dies mit der Liste und starten mit der kumulierten Binomial-Verteilung.

\(\\\)
Wir wählen \(\boxed{1}\)

\(\\\)
und noch einmal \(\boxed{1}\)

\(\\\)
Wir geben die Werte ein. Jede Eingabe wird mit \(\boxed{=}\) bestätigt. Nach der letzten Eingabe tippen wir erneut \(\boxed{=}\) .

\(\\\)
Wie zuvor verfahren wir bei der Eingabe mit den entsprechenden Werten. Abschließend wieder mit \(\boxed{=}\) bestätigen.

\(\\\)
Wir berechnen nun den Bereich mit
\( \quad \begin{array}{ r c l } P( 14 \leq x \leq 16) & = & P( x \leq 16) - P( x \leq 13) \\[4pt] & = & 0{,}984 - 0{,}7499 \\[4pt] & = & 0{,}2341 \\[4pt] & = & 23{,}41 \% \\ \end{array} \)
\(\\[1em]\)
Stelle k per Liste bestimmen
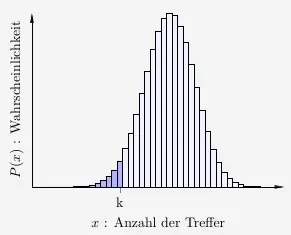
Gesucht wird eine Stelle \(k\), für die gilt
\( \quad P( x \leq k) \, \leq \, 0{,}05 \)
\(\\\)
mit
\( \quad \begin{array}{ r c l } n & = & 100 \\ p & = & 0{,}7 \\ \end{array} \)
\(\\[1em]\)
\(\\\)
Eine gesuchte Stelle \(k\) liegt grundsätzlich in der Nähe des Erwartungswertes. Wir ermitteln den Erwartungswert mit
\( \quad \mu \, = \, n \cdot p \, = \, 100 \cdot 0{,}07 \, = \, 70 \)
\(\\\)
In diesem Fall liegt \(k\) linksseitig von \(\mu = 70\). Wir probieren die zehn \(x\)-Werte darunter aus.
Wir starten wieder mit der Binomial-Dichte

\(\\\)
mit \(\boxed{4}\) und wählen die Liste

\(\\\)
mit \(\boxed{1}\) .

\(\\\)
Nach der Eingabe der Werte, siehe oben, bestätigen wir mit \(\boxed{=}\) .

\(\\\)
Mit Pfeil unten sehen wir die weiteren Werte.

\(\\\)
Wir sehen, dass
\( \quad P(x=66) \, = \, 0{,}0578 \, > \, 0{,}05 \)
\(\\\)
und
\( \quad P(x=65) \, = \, 0{,}0467 \, \leq \, 0{,}05 \)
\(\\\)
ist. Folglich ist die gesuchte Stelle \(k = 65\).
\(\\[1em]\)